Fluid Dynamics

Fluid Dynamics#

Spring 2025 revision

Author:
Date:
Time spent on this assignment:

import numpy as np
import matplotlib.pyplot as plt
import math
from matplotlib.animation import FuncAnimation
import itertools
from IPython.display import HTML
import pickle
def resetMe(keepList=[]):
    ll=%who_ls
    keepList=keepList+['resetMe','np','plt','math','FuncAnimation',
                       'HTML','itertools','pickle','testFunc']
    for iiii in keepList:
        if iiii in ll:
            ll.remove(iiii)
    for iiii in ll:
        jjjj="^"+iiii+"$"
        %reset_selective -f {jjjj}
    ll=%who_ls
    return

def testFunc(func,inFiles,outFiles):
    inputs  = [pickle.load(open(f,"rb")) for f in inFiles]
    outputs = [pickle.load(open(f,"rb")) for f in outFiles]
    result  = func(*inputs)
    allGood = True
    if not isinstance(result, tuple): result = (result,)
    for i in range(len(outputs)):
        if np.max(np.abs(result[i]-outputs[i])) > 1e-14:
            print("Failed test for",outFiles[i],i,np.max(np.abs(result[i]-outputs[i])))
            allGood = False
    if allGood: print("Test Passed!")
    else:       print("Test Failed :(")

Download the test files here, or download from the website and upload & unzip them to wherever this notebook file is

!wget https://courses.physics.illinois.edu/phys246/fa2020/code/TestFiles.zip && unzip TestFiles.zip

Python Warmup#

Useful functions:#

Before we begin, we want to highlight some functions that you may find useful in this assignment. The last one we’ll explore in more depth as well.

np.zeros([dimensions]) - create an array filled with all zeros. *Ex: n = np.zeros([9,10,10]) creates a (9,10,10) array of all zeros
np.ones([dimensions]) - same thing as np.zeros but with all ones.
np.empty([dimensoons]) - same thing as np,zeros but fills array with garbage. Very fast compared to the above.
np.roll(x,shift,axis) - shift array x by shift along axis.

Warmup - using `np.roll`#

Something we’ll see later in this assignment is the need to shift elements right,left,up,down, and diagonally. Let’s make a little test problem to illustrate how this works.

# Run me!
x = np.arange(15).reshape(3,5)
print(x)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]

Now we’ll want to shift every element in x to the right, where we wrap everything around the edge. Rather than figuring this out with a for loop, we’ll employ np.roll to do it fast!

print(x,'\n')
print(np.roll(x,(0,1),(0,1)))

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]] 

[[ 4  0  1  2  3]
 [ 9  5  6  7  8]
 [14 10 11 12 13]]

Now let’s disect that command. The first (0,1) means don’t shift the “y” direction, and to shift the “x” direction by +1. The next command, which should always be (0,1) means to apply the shift as a row, column matrix. Now let’s go left:

print(x,'\n')
print(np.roll(x,(0,-1),(0,1)))

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]] 

[[ 1  2  3  4  0]
 [ 6  7  8  9  5]
 [11 12 13 14 10]]

🦉 Now we’ll try to implement a section of the Cha-Cha Slide(Lyrics)

♫Now it's time to get funky
To the right now, to the left
Take it back now y'all♪

Make your x array go right, then left, then “down”. Your output should be:

[[ 4  0  1  2  3]
 [ 9  5  6  7  8]
 [14 10 11 12 13]]
[[ 1  2  3  4  0]
 [ 6  7  8  9  5]
 [11 12 13 14 10]]
[[ 5  6  7  8  9]
 [10 11 12 13 14]
 [ 0  1  2  3  4]]

(Notice how down isn’t what you may expect…)

#!Start
print(np.roll(x,(0,1),(0,1)))
print(np.roll(x,(0,-1),(0,1)))
print(np.roll(x,(-1,0),(0,1)))
#!Stop

[[ 4  0  1  2  3]
 [ 9  5  6  7  8]
 [14 10 11 12 13]]
[[ 1  2  3  4  0]
 [ 6  7  8  9  5]
 [11 12 13 14 10]]
[[ 5  6  7  8  9]
 [10 11 12 13 14]
 [ 0  1  2  3  4]]

🦉In a special version of the song, the next line goes

♫ Take it diagonally up and to the right now y'all

Implement this array move, you should get:

[[14 10 11 12 13]
 [ 4  0  1  2  3]
 [ 9  5  6  7  8]]

print(np.roll(x,(1,1),(0,1))) #!#

[[14 10 11 12 13]
 [ 4  0  1  2  3]
 [ 9  5  6  7  8]]

Now you’re a ~~Cha-Cha Slide~~ np.roll master!

Exercise 1: Fluid Dynamics#

List of collaborators:
References you used in developing your code:

In this assignment you will produce a fluid dynamics simulations. Our simulation is based on the lattice Boltzmann method. We will describe the microscopic behavior of the fluid using a 9-component model on a grid, which will be called n. Each of the 9 components represents a density of fluid moving in a different direction: stationary, up, down, left, right, and each of the diagonal directions. Propagation forward in time consists of three main steps:

Boundary conditions – In our case, we will assume periodic boundary conditions in the y direction (imagine a fluid in a torus), constant flow on the left, and smooth flow on the right.
Relaxation/collision – If some bits of fluid are moving right and some are moving left, they collide with each other at a certain rate.
Propagation/moving – Fluid that is moving right will move right and so on, and fluid bounces off any obstacles.

The macroscopic quantities density $\rho$ and overall velocity u just by summing up the amount and velocities of the microscopic fluid components in n.

We are going to develop a number of functions which you will store in the cell below (as well as some global variables that we will use throughout this exercise). Note that the only global variables you should ever use are constants, which in this exercise are nx,ny, and the velocities directions for each of the components v. Because they do not change in the entire workbook, it is reasonably safe to declare them as global variables.

The global variables are

nx=520; ny=180 #size of our simulation

### ANSWER HERE

If you have a function that takes in an array n, always make a new variable to return. This will allow you to compose functions, so that you can call f(g(n)) which will apply g to n and then f to the output of g.

def doMath(n):
    n[0,2] = 5 # this modifies n in place so the argument will also change. You don't want that. 
    # instead, do 
    nout = n.copy()
    nout[0,2] = 5
    nout = 2*n+5 # this makes a new object automatically
    return nout

a. Making some obstacles#

To simulate the real world on the computer, we’ll break the tunnel into $n_x\times n_y$ squares which we’ll call voxels.

Your simulation will be doing fluid dynamics in a $n_x \times n_y$ “tunnel” which has some objects within it. These objects will be represented by a boolean $n_x \times n_y$ size array obstacle=np.empty((nx,ny),dtype='bool') which should be True where the obstacle is and False otherwise. For example,

obstacle[:,:]=False
obstacle[50:70,50:70]=True

would set up a square $20 \times 20$ object inside our tunnel.

🦉Add a GenerateCylinderObstacle() function to the “function-cell” above which generates a object which is a cylinder located at $(n_x/4,n_y/2)$ with a radius of $n_y/9$

You can test it by calling

plt.matshow(GenerateCylinderObstacle().transpose())
plt.xlabel("")
plt.ylabel("")
plt.title("put title here")

It should look like this

Do not use the word object as a variable!
Notice how object is green in a cell - this means it is a special keyword.

b. Microscopic velocities $v_i$#

To simulate the real world on the computer, we’ll break the tunnel into $n_x\times n_y$ squares which we’ll call voxels.

The key quantity in your simulation is nine microscopic degrees of freedom

$n_k(i,j)$ where $0\leq k \leq 8$ and $(i,j)$ are over the $n_x \times n_y$ voxels of your simulation

which are going to be nine different densities (for each voxel $(i,j)$) which correspond to the density of a fluid at $(i,j)$ moving in nine different directions (or velocities $v_k$):

$n_0$: stationary fluid moving at velocity $v_0=(0,0)$
$n_1$: fluid moving up moving at velocity $v_1=(0,1)$
$n_2$: fluid moving down at velocity $v_2=(0,-1)$
$n_3$: fluid moving right at velocity $v_3=(1,0)$
$n_4$: fluid moving left at velocity $v_4=(-1,0)$
$n_5$: fluid moving left-down at velocity $v_5=(-1,-1)$
$n_6$: fluid moving left-up at velocity $v_6=(-1,1)$
$n_7$: fluid moving right-down at velocity $v_7=(1,-1)$
$n_8$: fluid moving right-up at velocity $v_8=(1,1)$

It will be useful to have access to these microscopic velocities as global variables. 🦉Go ahead and add to the top of your “function-cell” the various velocities:

v=np.zeros((9,2),dtype='int')
v[0,:]=[0,0]
v[1,:]=[0,1]
...

Plot these (below) as

for i in range(0,9):
    plt.arrow(0,0,v[i,0],v[i,1],head_width=0.05, head_length=0.1, fc='k', ec='k')
plt.xlim(-1.2,1.2)
plt.ylim(-1.2,1.2)
plt.show()

and make sure it looks like

We will represent the microscopic densities by a variable

n=np.zeros(9,nx,ny)

The high level algorithm for fluid dynamics is very simple. After setting up the initial conditions, we loop many times doing

Adjust boundary conditions
Collide the microscopic densities
Move the microscopic densities

c. Computing macroscopic quantities from the microscopic density#

Given the microscopic densities, there are two macroscopic quanties:

the macroscopic density $\rho(i,j)=\sum_k n_k$ (size: $n_x \times n_y$)
the macroscopic velocity $\vec{u}(i,j) \equiv (u_x(i,j),u_y(i,j))$ (size: $2 \times n_x \times n_y$) where
- $u_x(i,j) = 1/\rho \sum_k v_{k,x} n_k(i,j)$
- $u_y(i,j) = 1/\rho \sum_k v_{k,y} n_k(i,j)$

which you will compute using the function (you will write) (rho,u) = Micro2Macro(n)

🦉Go ahead and write this function and add it to your ‘function-cell’

You can test it using these lines of code:

testFunc(Micro2Macro,["Microscopic.dat"],["rho_after_Micro2Macro.dat","u_after_Micro2Macro.dat"])

and see if it print two zeros (which is a success!)

Tip: Because u is $(2,n_x,n_y)$, we can get ux by doing u[0] (which is then a $(n_x,n_y)$ array) and uy by doing u[1].

optional - `np.einsum`#

Figuring out the summations efficiently can be a pain, but we can use np.einsum help out here. Figure out how to rewrite the above problem with Einstein summation notation. To use the function, if we have $$ A_{ijk}\cdot B_{dk} = C_{ijd}, $$ we’d use then call:

C = np.einsum("ijk,dk->ijd",A,B)

d. Getting the equilibrium microscopic densities.#

Given the macroscopic densities $\rho$ and $\vec{u}$, there is a equilibrium microscopic densities $n_{eq}$ (size: $9 \times n_x \times n_y$) which you will compute using n_eq=Macro2Equilibrium(rho,u)

The relevant formula for this is

\[ n^{eq}(v_k) \equiv n_k^{eq} = \omega_k \rho \left(1 + 3 \vec{v_k} \cdot \vec{u} + \frac{9}{2}(\vec{v_k} \cdot \vec{u})^2- \frac{3}{2}(\vec{u}\cdot \vec{u}) \right) \tag{A} \]

where

$\omega_{0}=4/9$
$\omega_{1-4}=1/9$
$\omega_{5-8}=1/36$

Given some microscopic densities $n$ you should be able then to figure out the equilibrium microscopic densities $n_{eq}$.

🦉Write the functions Macro2Equilibrium adding them to your “function-cell”

You can test it by checking if

testFunc(Macro2Equilibrium,["rho_after_Micro2Macro.dat","u_after_Micro2Macro.dat"],["Microscopic_after_equilibrium.dat"])

is equal to zero.

d. Implementing collision#

Once you can compute these quantities, the next step is to implement the collision step.

🦉Write a function Collision(n,obstacle) which returns the density n after collision. Put it in your function-cell above.

When we collide the microscopic densities, we get new microscopic densities given as

nout = n * (1-omega) + omega * neq

Here are the steps for the function: $\phantom{}$

Calculate neq
a. take the microscopic densities $\rightarrow$ compute the macroscopic density and velocity (rho,u) = Micro2Macro(n)
b. take the macroscopic density and velocity $\rightarrow$ compute the equilibrium microscopic densities neq=Macro2Equilibrium(rho,u)
Calculate nout = n * (1-omega) + omega * neq
a. $\omega$ is the viscosity parameter. We will use $\omega =1.9572953736654806$
We moved fluid where the obstacle is, so we need to undo this. Reset all nout where the obstacle is to be the same as n

Test with

testFunc(lambda x: Collision(x,GenerateCylinderObstacle()),["Microscopic.dat"],["Microscopic_after_collision.dat"])

e. Moving#

We’ll now move on to getting the fluid to move. This will be a function called, surprise, Move(n,obstacle). But first we need to helper functions:

Bounce(n,obstacle)
- bounce the velocities - that is every velocity where the obstacle is gets reversed
MoveDensity(n)
- Move all your densities in the direction of the velocity (hint the velocity tells you where to move it)
- Assume periodic boundary conditions here

🦉 Implement Bounce(n,obstacle) -> nout

bounce the velocities off the – every velocity where the obstacle is gets reversed

🦉 Implement MoveDensity(n) -> n

Move all your densities in the direction of the velocity (hint the velocity tells you where to move it)
Assume periodic boundary conditions here

🦉 Test using

testFunc(MoveDensity,["Microscopic.dat"],["Microscopic_after_moveDensity.dat"])

Move(n,obstacle) call is just a Bounce then MoveDensity.

🦉Write this function and test!

testFunc(lambda x: Move(x,GenerateCylinderObstacle()),["Microscopic.dat"],["Microscopic_after_move.dat"])

f. Boundary conditions#

In the y-direction, we are just going to assume that the boundary conditions are periodic. For the x-direction, we are going to assign certain boundary conditions on the left and right.

Let’s call this function FixBoundary(n,n_init) which applies these boundary conditions and returns the new density n.

Left: we are going to assume that there is a flow - this means that the microscopic densities are the same at each step. Therefore, what we should do is simply replace the current densities on the left-most row with the initial microscopic densities (n_init).

Right: we are going to assume that the gradient is zero - i.e. the important physics has dissapeared by this point. To do this, we will set

# loop over all microscopic velocities vL that are going left 
   nout[vL,-1,:] = nout[vL,-2,:] 

Hint: there are 3 vLs.

🦉Put all of this together and run the next test!

Testing:

testFunc(FixBoundary,["Microscopic.dat","Microscopic2.dat"], ["Microscopic_after_boundary.dat"])

g. Setting up the initial conditions#

We need to generate an initial conditions. The way that we are going to do that is

pick some macroscopic density $\rho$ of size $(n_x,n_y)$ (uniformly equal to 1.0) and a
macroscopic velocity $\vec{u}(i,j)$ (sizes $(2,n_x,n_y)$)
- 0.04*(1.0+1e-4*np.sin(y/(ny)*2*np.pi)) in the x-direction (aka 0). This introduces a very tiny anisotropy to the system.
- zero in the y-direction (aka 1)
compute the equilibrium density $n_{eq}$ associated with the initial density and velocities.
Use (and return) this as the initial conditions

🦉Write a function Setup() which returns the initial microscopic densities. Remember to save this as you will need it to apply your boundary conditions.

I get the following when I visualize it as plt.matshow(Setup()[3].transpose())

A quick test here is just to check that the following:

print("All good?",(np.abs(np.max(Setup())-0.443377991)<1e-5) and ((np.abs(np.min(Setup())-0.0245774711)<1e-5)))

h. Putting it all together#

🦉Write a function Run(steps,record,n,n_init,obstacle) (up in your function-cell) which takes

the number of steps steps you want to run
how often you want to record the velocity and density
the microscopic densities n to start running from
the initial microscopic densities n_init for the boundary conditions (often equal to n.copy())
obstacle boolean array obstacle.

Each step consists of:

Adjust boundary conditions FixBoundary
Collide the microscopic densities Collision
Move the microscopic densities Move

It should return

a list of macroscopic densities rhos (this should be a list of $n_x \times n_y$ arrays)
a list of macroscopic velocities us = $\sqrt{\vec{u}\cdot\vec{u}}$ (this should be a list of $n_x \times n_y$ arrays)
the last microscopic density n (this should be a single array of size $9\times n_x \times n_y$)

It should run like the following

n_in=Setup()
n_init=fin.copy()
obstacle=GenerateCylinderObstacle()
rhos, us, n_final = Run(steps=200, record=100, n_in, n_init, obstacle)
plt.matshow(us[-5])
plt.show()
...

🦉Run for 2001 steps recording every 100 steps. Then plot the final 5 us.

i. Animation of a long simulation#

First we will do a long calculation. This might take a while so we will run

fins=rhos=us= [None] * 21
fins[0]=n_in.copy()
for i in range(0,20):
    %time (rhos[i],us[i],fins[i+1])=Run(2001,100,fins[i],n_init,obstacle)

which will generate our data.

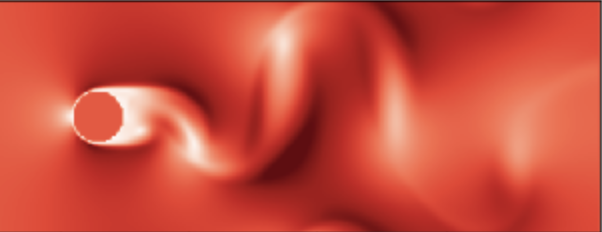
🦉Now write a function AnimateMe(us_flat,vMax) which is going to take a list of velocities us_flat (and maximum for the vMax) and going to return an animation which is going to be then produced by calling

us_flat = list(itertools.chain.from_iterable(us[:-1]))
anim = AnimateMe(us,vMax)
HTML(anim.to_jshtml())

The first line converts the list of lists into a single iterable.

This function will look like:

def AnimateMe(us_flat,vMax):
    fig, ax = plt.subplots()
    cax = ax.imshow(us_flat[1],cmap=plt.cm.Reds,vmin=0,vmax=vMax)
    plt.close(fig)
    def animate(i):
         cax.set_array(us_flat[i])

    anim = FuncAnimation(fig, animate, interval=100, frames=len(us_flat))
    return anim

j. Speed Test ( 5 points extra credit)#

Our code for for %time Run(2000,3000,Setup(),Setup(),GenerateCylinderObstacle()) takes between 45 and 60 seconds. We’ll give 5 points if you can make your code faster than 40 seconds runtime (on the server). Warning: we aren’t sure this is possible!

Exercise 2: Walls#

List of collaborators:
References you used in developing your code:

In this exercise we are going to use all the same code but generate a different object. Here generate an object which consists of two walls:

one spans $50 \leq x \leq 60$ and $n_y/4 \leq y \leq 3n_y/4$
the other spans $200 \leq x \leq 210$ and $n_y/4 \leq y \leq 3n_y/4$

🦉Run your code again with this new obstacle and generate a new animation.

# Generate data here

# Animation code

Exercise 3: Something new… (EC)#

(Extra credit: 5 points)

List of collaborators:
References you used in developing your code:

🦉Come up with something new and cool to do with this animation code. Maybe try out some other interesting obstacles are add some friction to the walls or such.

Answer:#

Acknowledgement: This assignment originally inspired from code from flowkit.com

Bryan Clark (original)

# You can safely ignore these lines; they are just to generate the test files.
#import pickle
#np.random.seed(30)
#microscopicDensity=np.random.random((9,nx,ny))
#pickle.dump( microscopicDensity, open( "Microscopic.dat", "wb" ) )
#(rho,u)=Micro2Macro(microscopicDensity)
#pickle.dump( rho, open( "rho_after_Micro2Macro.dat", "wb" ) )
#pickle.dump( u, open( "u_after_Micro2Macro.dat", "wb" ) )

#pickle.dump( microscopicDensity, open( "Microscopic_after_equilibrium.dat", "wb" ) ) #!#


#pickle.dump( Collision(microscopicDensity,GenerateCylinderObstacle()), open( "Microscopic_after_collision.dat", "wb" ) ) #!#


#!Start
#pickle.dump( MoveDensity(microscopicDensity), open( "Microscopic_after_moveDensity.dat", "wb" ) )
##pickle.dump( MoveDensity(microscopicDensity,GenerateCylinderObstacle()), open( "Microscopic_after_collision.dat", "wb" ) )
##print(np.max(np.abs(Collision(microscopicDensity,GenerateCylinderObstacle())-pickle.load( open( "Microscopic_after_collision.dat", "rb" ) ))))
#microscopicDensity=pickle.load( open( "Microscopic.dat", "rb" ) )
#pickle.dump( Bounce(microscopicDensity,GenerateCylinderObstacle()), open( "Microscopic_after_bounce.dat", "wb" ))
#microscopicDensity=pickle.load( open( "Microscopic.dat", "rb" ) )
#pickle.dump( Move(microscopicDensity,GenerateCylinderObstacle()), open( "Microscopic_after_move.dat", "wb" ) )
#!Stop


#!Start
#microscopicDensity2=np.random.random((9,nx,ny))
#pickle.dump(microscopicDensity2,open( "Microscopic2.dat","wb"))
#pickle.dump( FixBoundary(microscopicDensity,microscopicDensity2), open( "Microscopic_after_boundary.dat", "wb" ) )
#!Stop

Fluid Dynamics

Contents

Fluid Dynamics#

Python Warmup#

Useful functions:#

Warmup - using `np.roll`#

Exercise 1: Fluid Dynamics#

a. Making some obstacles#

b. Microscopic velocities \(v_i\)#

c. Computing macroscopic quantities from the microscopic density#

optional - `np.einsum`#

d. Getting the equilibrium microscopic densities.#

d. Implementing collision#

e. Moving#

f. Boundary conditions#

g. Setting up the initial conditions#

h. Putting it all together#

i. Animation of a long simulation#

j. Speed Test ( 5 points extra credit)#

Exercise 2: Walls#

Exercise 3: Something new… (EC)#

Answer:#

Fluid Dynamics

Contents

Fluid Dynamics#

Python Warmup#

Useful functions:#

Warmup - using np.roll#

Exercise 1: Fluid Dynamics#

a. Making some obstacles#

b. Microscopic velocities \(v_i\)#

c. Computing macroscopic quantities from the microscopic density#

optional - np.einsum#

d. Getting the equilibrium microscopic densities.#

d. Implementing collision#

e. Moving#

f. Boundary conditions#

g. Setting up the initial conditions#

h. Putting it all together#

i. Animation of a long simulation#

j. Speed Test ( 5 points extra credit)#

Exercise 2: Walls#

Exercise 3: Something new… (EC)#

Answer:#

Warmup - using `np.roll`#

optional - `np.einsum`#